欢迎来到中国矿山建设第一门户网站！
算
吴远迪1，龙志阳2，周志鸿1
（1.北京科技大学；2.北京中煤矿山工程有限公司）
摘 要：抓岩机是一种矿山建井设备，在井下抓取岩石装入吊桶中并提升出井实现排矸，其工
况类似起重机。以目前最新研制的斗容 1m3大型抓岩机的吊臂为对象，利用 Pro/E建立其三维实体模型，并将模型导入ADAMS，仿真吊臂变幅的运动过程，求得吊臂加速吊起岩石过程中承受的动载荷。把动载荷中的最大值加载到吊臂上，利用 ANSYS Workbench 进行吊臂有限元分析，将动力学问题转化为静力学问题来处理，判断吊臂的刚度和强度是否满足要求。
关键词：抓岩机吊臂；ADAMS；动载荷；ANSYSWorkbench
目前国内使用较多的抓岩机为 HZ 型中心回转气动抓岩机，斗容有 0.1～0.6 m3多种型号，本文讨论的抓岩机为国内首台液压驱动，抓斗容积为 1 m3的大型中心回转抓岩机。该机液压驱动可提供足够的动力，并简化了驱动部分结构，再配上 1 m3 抓斗， 使得其抓岩能力和效率大大提高，加快了建井速度。吊臂为整个抓岩机受力最危险部分，以往 HZ 型抓岩机曾发生过吊臂断裂，导致人员伤亡的事故， 因此对抓岩机吊臂进行动力学分析非常必要。
利用 Pro/E建立抓岩机吊臂三维模型，通过专业接口 Mechanism/Pro 将其导入 ADAMS，并使吊臂的运动处于XY 平面内，如图 1 所示。导入之前要设置模型的密度，长度单位要做相应的转换。模型主要包括机架、液压缸、吊臂和销轴等刚体。
如图 1 所示，机架上部固定，吊臂尾部与机架通过销轴连接，中间被液压缸活塞杆支撑，吊臂前部通过钢丝绳吊起重物，吊起的重物为抓斗和岩石。由于钢丝绳较长（10 m），图1 中未将重物显示
出来。液压缸伸缩使吊臂产生变幅运动，图 1 所示位置为活塞杆全伸出的情况，此时液压缸与吊臂接近垂直，吊臂起吊幅度最大，活塞杆全缩回时，吊臂起吊幅度最小。
| 图 1 三维模型导入ADAMS |
2.1 静态计算
吊臂受力如图 2 所示，此时吊臂起吊幅度最大，随着起吊幅度的减小，重物的拉力和液压缸推力对 A 点的力臂均减小，不能判断在哪一个起吊幅度下吊臂承受的液压缸推力最大。最大起吊幅度时对铰点A 取矩：
G1×L G2×2 631.3=F×1 080.4 （1）
式中：G1—吊臂自重，2 866 N；
G2—吊臂提升的重量，与抓斗自重和岩石重量有关，通过计算取 60 000 N ；
F——液压缸的推力，N；
L——吊臂重力到铰点 A 的力臂，mm。
由于 L 不易确定，假设吊臂重心在吊臂中部，取 L=1 250 mm，可得：
F×1 080.4=G2×2 631.3 G1×1 250 F=149.4 kN
2.1 ADAMS 动态仿真
模型导入 ADAMS之后，首先设置重力加速度和各刚体之间的约束，然后添加吊臂的驱动。机架上部固定，吊臂与机架销轴之间用旋转副连接，液压缸两头均为旋转副，活塞与液压缸之间为圆柱副，钢丝绳与销轴之间为旋转副，钢丝绳与重物之间为球副。
变幅时吊臂由液压缸驱动，而液压缸活塞的运动速度根据液压系统的流量来换算，考虑吊臂起吊幅度由小增大的过程，此时大腔进油，由于是双液压缸驱动，流量与速度的关系式如下：
v2=φ×v1=0.224 m/s
活塞杆的运动有加速运动、匀速运动和减速运动，其运动可用阶跃函数来控制：
STEP(time, 0.0,- 224, 3.2,- 224）
STEP(time, | 3.2, | 0, | 4.0, 224） |
STEP(time, | 4.0, | 0, | 8.0, 0） |
STEP(time, | 8.0, | 0, | 8.5, 112） |
STEP(time, 8.5, 0,15.2, 0）
STEP（time,15.2, 0,15.7, - 112）
函数时间单位为 s，速度单位 mm/s。考虑到液压缸的缓冲作用，假设加速和减速时间在 0.5 s 左右，阶跃函数使得吊臂的起吊幅度由最大变到最小，然后再增到最大，如果在模型上去掉重物和钢丝绳，用一个与其重力方向相同，大小为60 000 N 的力代替，则最大起吊幅度时分析结果与静态计算结果接近，通过仿真可得到吊臂起吊幅度变化曲线、液压缸推力曲线和吊臂加速度曲线如图 3、图 4 和图 5 所示。
1 × πD2×v1 = Q × 1 × 1
（2）
4 10 000 2 1 000 60
由驱动函数可知，0~4 s 减幅运动完成，4~8 s 是中间停顿时间，8~15.7 s 为增幅过程，吊臂回到原来的位置。图 3、图 4 显示，液压缸推力根据吊臂起吊幅度变化而变化，液压缸收缩过程中，起吊幅度由60.8°减小到15°，重物的力臂减小，液压缸的推力变小，可见推力随着起吊幅度单调变化。
液压缸推力最大值为 149.7 kN，运动过程平稳。这个值与静态计算结果相近，证明了动态仿真的可靠性，从图 5 可知吊臂做加速运动，加速度最大值在 1 320 mm/s2 左右，较大的 3 个峰值是在驱动变速时产生的。
抓岩机吊臂实际运行中还要考虑重物的加速运动，取抓斗和岩石的总质量为 6 000 kg（这个值会因抓取的岩石量的不同而有所变动）。加上重物再次仿真，得到液压缸的推力曲线和重物对吊臂在 Y 方向的作用力曲线如图 6 和图 7 所示。
图 6 表明变幅过程中液压缸的推力不再是单调下降或上升，4 s 左右推力突然上升；从图 7 可看出推力的突然变化是由于重物的加速运动造成，此时重物对吊臂的作用力有一个较大的峰值。液压缸推力最大值上升到 155.4 kN 且有波动，导致整个变幅过程平均推力增大，由阶跃函数知15.7 s 后液压缸停止了运动，但重物仍然在摆动。液压缸推力的大小和波动情况是液压系统设计时必须考虑的。
重物水平惯性载荷较小，可忽略不计。由图 7
知重物对吊臂在 Y 方向的最大作用力为 63.1 kN。
进行吊臂的强度和刚度校核时，可利用这个力为有 设
限元分析提供更合理的载荷值。
2ANSYSWorkbench 分析 算
2.1 刚体材料参数设置
把三维模型导入 ANSYS Workbench，并设置材料为 Q235，屈服极限 235 MPa，抗拉极限为 460 MPa，弹性模量 E=2.1e5 MPa，泊松比 μ=0.3。
2.2 刚体连接设置
吊臂机架上的销轴可自由转动，液压缸与吊臂的销轴铰接。上述连接均采用 no separation 方式，若刚体受力不平衡，会引起较小的相对滑动，但物体间法向不会发生分离。
2.3 网格划分
由于机架的设计完全能满足强度和刚度的要求，因此校核时不考虑机架部分，仅对吊臂及其连接部分进行网格划分，自动选择 solid 186 和 solid 187 单元，统计得节点数 31 050，单元数 15 083。由于不考虑机架，大大减少了分析所需的时间。
2.4 添加载荷约束进行仿真
添加载荷约束，销轴与机架固定，设置好各刚体的连接，取重物对吊臂的载荷最大值 63.1 kN，进行有限元分析。分析结果如图8、图 9 所示。
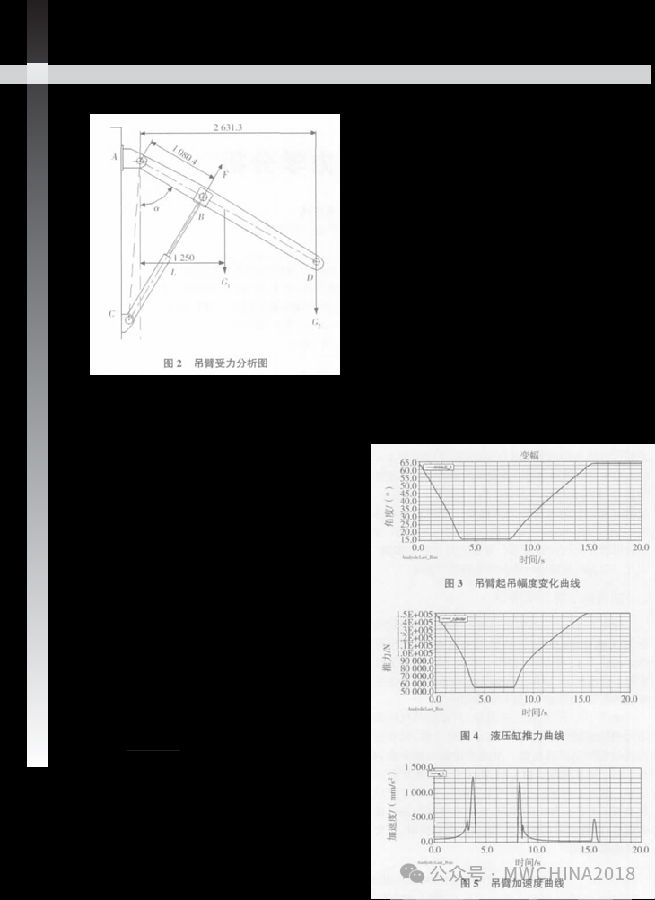
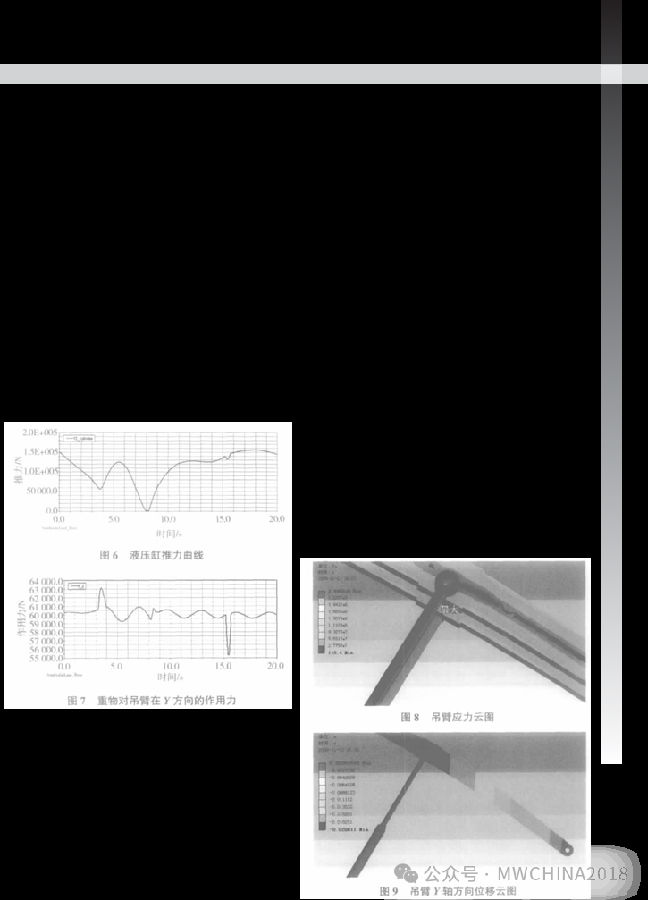
图 8 表明，液压缸上应力值小，最危险位置在
| 计 |
设 吊臂上活塞杆支撑点的底部，最大应力值为 249.8
MPa。虽然设计者专门在此处上、下两面各焊上了一计 块围板，但此处应力值仍然过大，超过了材料的屈算 服极限 235 MPa，其周围多处黄色区域应力值在
200 MPa 左右，安全系数小。
图 9 表明在液压缸支撑点往后，吊臂 Y 方向位移只有 0.6 mm，而在支撑点以前沿 Y 轴方向的位移最大是 - 20.6 mm。根据标准，悬臂梁（长度为L）的挠度限值为L/250。吊臂从支点到最外端的长度为2 000 mm，因此梁限定的最大位移为 8 mm。支撑点以前沿Y 轴方向的位移超标，吊臂设计不合理，刚度不够，吊臂结构需要改进。
材料不变，改进的方案主要有：
1） 吊臂上、下围板的厚度加厚 4 mm；
2） 吊臂的宽度增加 15 mm；
3） 两吊臂之间的距离增加 60 mm；
4）在不影响起吊幅度的前提下，两侧液压缸支撑点适当向外移动。
结构改进后，其他参数均不变，仿真发现变截面处有小范围的红色区域，表明有应力集中，最大应力为 161.9 MPa，此处应加上过渡圆角，其余应力较大的地方，应力值的范围在 110~140 MPa 之间， 相比改动之前明显减小，提高了安全系数。吊臂位移最大值为 - 5.08 mm，小于挠度限定值 8 mm。由此可见，改进后抓岩机的吊臂的受力和变形均优于之前的设计方案，且满足设计要求。
参考文献
[1]杨占尧.Pro/E 2.0 产品造型与模具设计精解及案例[M]. 北京：化学工业出版社，2005．
[2]李兵，何正嘉，陈雪峰.ANSYS Workbench 设计、仿真与优化[M].北京：清华大学出版社，2008．
[3]李增刚.ADAMS 入门详解与实例[M].北京：国防工业出版社，2008．
[4]李丹, 周志鸿，刘瑞华.基于ANSYS 液压挖掘机动臂的有限元分析[J].建筑机械，2008（9）：74- 78．
[5]杜中华，薛德庆，赵迎江.Pro/E 和ADAMS 传递过程中若干问题的讨论[J].机械与电子，2003（2）：67- 69．
通信地址：北京市海淀区学院路 30 号 北京科技大学土木与环境工程学院（100083） （收稿日期：2010- 01- 27）
您当前所在位置：